I love teaching Geometry, love all the activities that I jam pack into every period. This past week we delved into the subject of transformations. I know in other districts this topic is taught later in the year but for some reason our textbook puts it in the second module to teach.
I find it fun; students are a little dazzled because there are three different types and they can’t get them straight. At the beginning of the week, I changed the seating charts. Yes, I know that some teachers like to give the students free rein to sit where they like, but I like to make the most of my instructional time. So, when I use a seating chart, I can get the attendance taken in 20 seconds or less. Without one, I spend 5 minutes or more trying to find all the students.
Transformations in real life
The change in the seating chart gave me a perfect introduction to the unit. Some students were reflected from one side of the room to the other while other students were translated. But none of the students were rotated. I asked them which transformation their new seat best represented, and most could understand in these terms. One student claimed he was rotated—by 360 degrees! I guess I can’t argue with that.
Notations for Transformations
Coordinate notation and vector notation were the first hurdles. There is some confusion with coordinate notation. They believe that (x +5, y + 1) means that the new ordered pair is (5,1) so they needed more practice. I dislike worksheets, I hate to see kids quietly working at their desks so a lot of activities I create involve talking and moving. The treasure hunt was the perfect practice.
Transformation Activity
I posted the 8 problems around the room. Students could begin anywhere, do the first problem and when they had the answer, they had to look for their answer on another page. See at the bottom where it says, “previous answer”. This makes the activity self-checking. I ask them to note the new coordinates on their answer sheet and put the letters as they visit each page. This makes my checking easier.
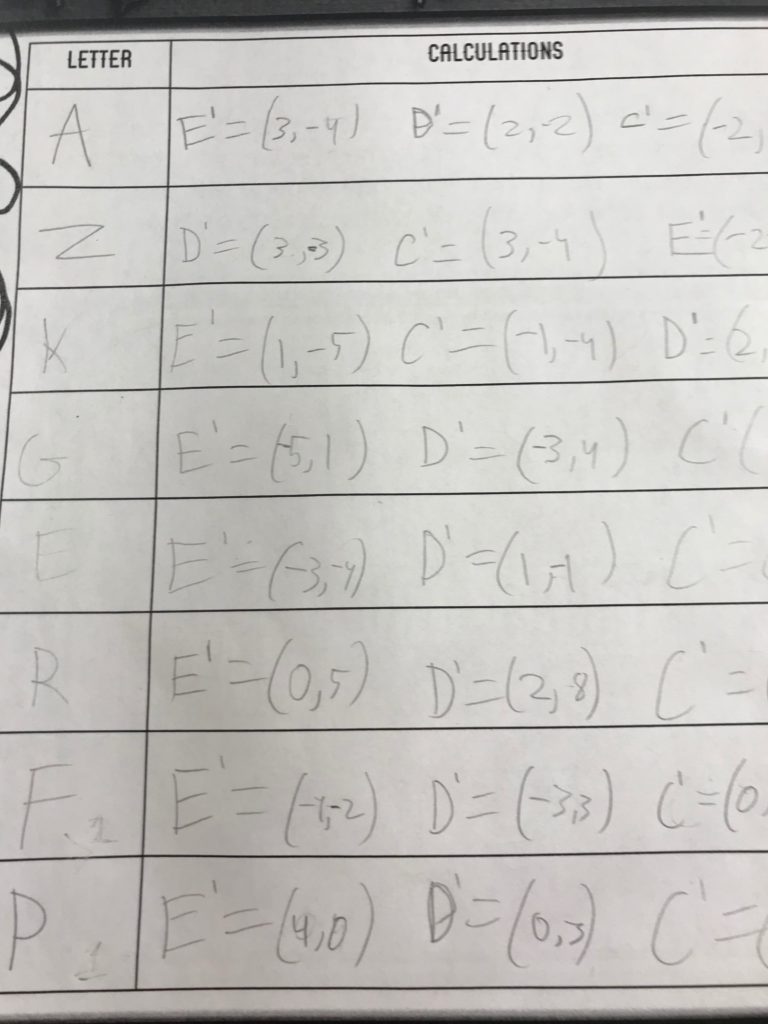
However, some students evidently thought the random letters I used to make the checking easier spelled a word. They wasted a lot of time trying to find a word that uses the letters “G R A Z P F E K”. So, in other classes I was clear that this isn’t a boggle game, no words are being spelled.
This is not an activity that I have listed on my Teachers Pay Teachers store. If you think your students would benefit from this activity, you can have a copy by clicking here.
Transformations are easy but don’t say so
On Wednesdays, we have a late start to facilitate collaboration in course-alike groups, so all the periods are shortened to 35 minutes each. It was perfect for this 8-problem activity. I had to demonstrate what to do and I still managed to confuse them but when 30 minutes was up, they all had it done. My second period got into a heated argument over the math—wow, that was a new one. But they figured it out as well and then told me how easy it was.
Years ago, I used to tell the kids “this is easy” thinking that this would be motivating, but one student in the end of the year survey pointed out they hate when teachers say something is easy when it isn’t—makes them feel stupid. So, I never say that anymore.
Reflections and Patty Paper
For reflections and rotations, I used patty paper. I laminated some printed coordinate planes and have the students use white board markers to draw a figure (triangle, rectangle, pentagon), label the vertices and then draw the figure on patty paper and either reflect or rotate. Some students have difficulty with Geometry because while they may be visual learners, their spatial ability is not fully developed yet. Patty paper gives them a hands-on activity that they can see and feel. For some students this will make the difference in understanding.
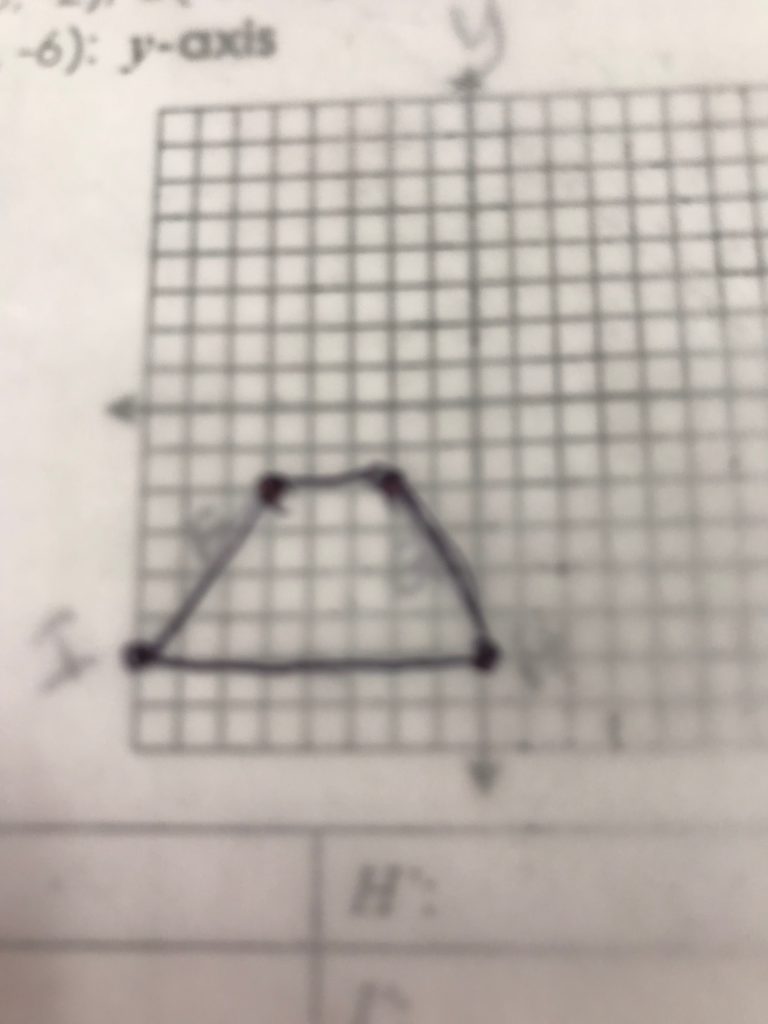
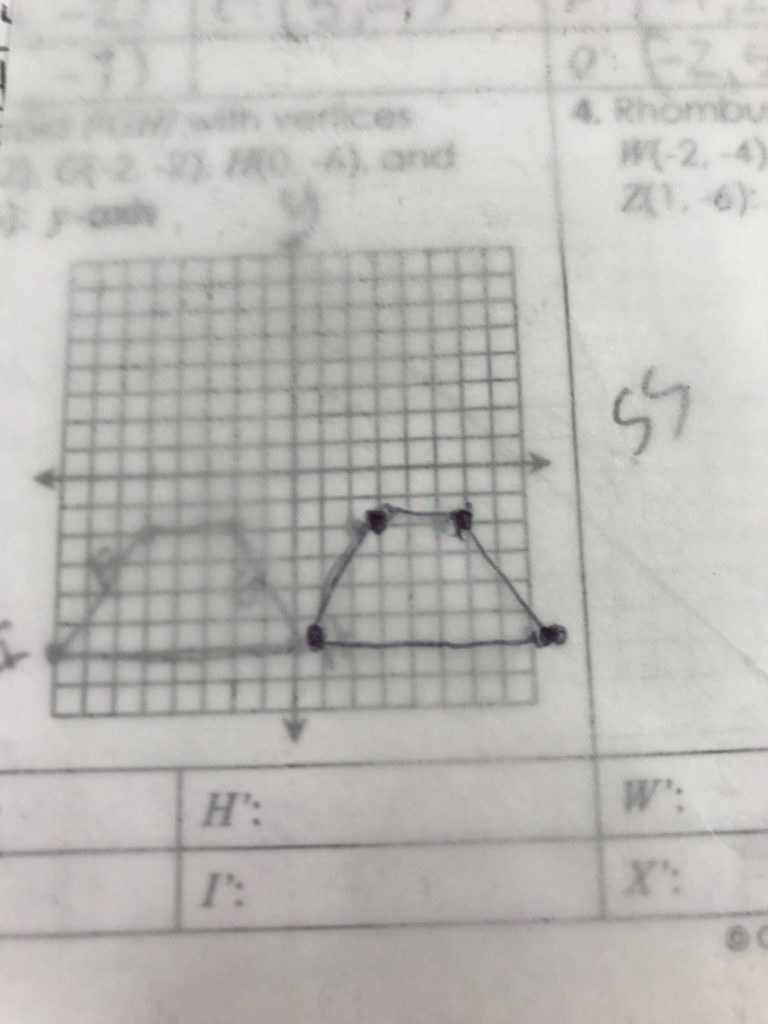
The patty paper makes it look blurry. Did you know that you can trace the figure and then turn it over, place it in position and then just either rub it or make a point again and the original markings will transfer? This came in handy for some students. I know reflections are easier for students to understand, but I like to use different tools so students can see there is always more than one way to get an answer.
Students are also struggling with language so I make some sentence stems to help them explain their sequences. Students are still using non-academic language to describe rotations and reflections especially.
They use the words, turn and flip and lack precision that is expected in our curriculum assessments. After dwelling on this and modeling it several times, I decided sentence stems were the answer. However, when they were given 3 difference sequences to describe, all the students reverted to their own descriptions. The second sequence they incorporated more descriptions and by the third they had embraced the sentence stems given to them.
I rotated ___#____ degrees ____Direction__________ around point _________, then _________
I reflected over the segment _____________________, then ________
I translated by segment _________________, then ___________…
I will definitely use more sentence stems to help students develop the vocabulary and explain what they are doing. Do you use sentence starters in the classroom and what has been the result? Drop a comment or email me at bluemountainmath@gmail.com.
Loved the Stand Up/Sit Down activity!